Es una técnica de modelado (construcción de modelos).
Es una técnica matemática de optimización, esto es,buscar maximizar o minimizar una meta u objetivo. Su fin es calcular el resultado óptimo que será el fundamento de la toma de decisiones.
Secuencia de construcción y solución en programación lineal:
- Construcción del modelo
a) Identificación de variables de decisión
b) Determinación de la función objetivo
c) Establecimiento de restricciones
- Solución gráfica
- Solución analítica
Estructura básica de un modelo de programación lineal
- Función objetivo
- Función a optimizar (maximizar o minimizar)
- Restricciones
Representan condiciones que se deben respetar o satisfacer. Dado por un sistema de igualdades y des igualdades (≤ o ≥).
La programación lineal es un procedimiento o algoritmo matemático mediante el cual se resuelve un problema indeterminado, formulado a través de un sistema de inecuaciones lineales,optimizando la función objetivo, también lineal.
Consiste en optimizar (minimizar o maximizar) una función lineal, denominada función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de restricciones que expresamos mediante un sistema de inecuaciones lineales.
Las variables son números reales mayores o iguales a cero. 
En caso que se requiera que el valor resultante de las variables sea un número entero, el procedimiento de resolución se denomina Programación entera.
Las restricciones pueden ser de la forma:
Tipo 1: 
Tipo 2: 
Tipo 3: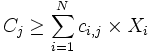 
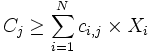
Donde:
- A = valor conocido a ser respetado estrictamente;
- B = valor conocido que debe ser respetado o puede ser superado;
- C = valor conocido que no debe ser superado;
- j = número de la ecuación, variable de 1 a M (número total de restricciones);
- a; b; y, c = coeficientes técnicos conocidos;
- X = Incógnitas, de 1 a N;
- i = número de la incógnita, variable de 1 a N.
En general no hay restricciones en cuanto a los valores de N y M. Puede ser N = M; N > M; ó, N < M.
Sin embargo si las restricciones del Tipo 1 son N, el problema puede ser determinado, y puede no tener sentido una optimización.
Los tres tipos de restricciones pueden darse simultáneamente en el mismo problema.
La función objetivo puede ser:
o
Donde:
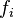= coeficientes son relativamente iguales a cero.
BIBLIOGRAFIA
Material proporcionado por el Mtro. Arturo Vázquez Flores
No hay comentarios.:
Publicar un comentario